Friday, 25 July 2014
And my version of the exercises spreadsheet is in the same shared area...
In the shared folder (link).
Labels:
Second Week
Exercise: Network with Diminishing Returns
Goal To model/graph demand characteristics for a network market with diminishing returns or a saturation effect.
At least one laptop or tablet running a spreadsheet application for each group.
Individuals or groups of 2 or 3 students working on a single computer.
You will need basic knowledge of: spreadsheet calculations, sum, addition, multiplication, bracket rules, cell ranges, relative cell references, absolute cell references etc.
Up to one hour to complete depending on class size, i.e.
20-30" to create models.
10-20" to present and interpret.
Instructions
Open and save a spreadsheet: enter formulae, values and calculations to create a graph representing a network market with positive feedback.
a) Enter the following data in columns and generate line or scatter graphs:
Consider a network market of expected size N (e.g. users anticipate up to 50 people in a market for some good), where each user's intrinsic propensity to purchase is a value v uniformly distributed over the unit interval, i.e. v: [0, 1]. In this case we will model a network market where the actual value obtained by the nth user will be Vn=v*(n-1)*NMaterials
At least one laptop or tablet running a spreadsheet application for each group.
Individuals or groups of 2 or 3 students working on a single computer.
You will need basic knowledge of: spreadsheet calculations, sum, addition, multiplication, bracket rules, cell ranges, relative cell references, absolute cell references etc.
Up to one hour to complete depending on class size, i.e.
20-30" to create models.
10-20" to present and interpret.
Instructions
Open and save a spreadsheet: enter formulae, values and calculations to create a graph representing a network market with positive feedback.
a) Enter the following data in columns and generate line or scatter graphs:
- A column containing an index n representing the number of users e.g. from 1 to 50, i.e. up to the Expected Network Size N= 50.
- A column containing the individual's reservation value v, i.e. a demand function for each person, uniformly distributed over the interval [0, 1]
- A column containing value of a network of expected size N to the nth user; also the point at which actual network size is also n. The price or willingness of the nth user to pay i.e. Vn = v*(n-1)*N
- A column containing the actual value of the network at size n, i.e. VT = n*Vn, where Vn = v*(n-1)*N
Your models should look something like this:
 |
| Demand/supply curve with uniformly distributed demand (N=43) |
b) For the same interval N graph the demand/supply curve for a demand function representing the classic 'three types of customer' model i.e. where v3types: [1.0, 0.5, 0.02]; in the following ratios: Spend Thrifts 10% (v3types = 1.0), Average Spenders 60% (v3types = 0.5), Tight Wads 30% (v3types =.02).
- Add a column containing value of a network of expected size N to the nth user; also the point at which actual network size is also n. The price or willingness of the nth user to pay i.e. Vn3types = v3types*(n-1)*N
- Add column containing the actual value of the network at size n, i.e. VT3types = n* Vn3types, where Vn3types = v3types*(n-1)*N
A graph of 'three types of customer' model only:
 |
| Network value for 'three types of customer' model |
Or combining both uniform distributed demand and the classic 'three types of customer' model:
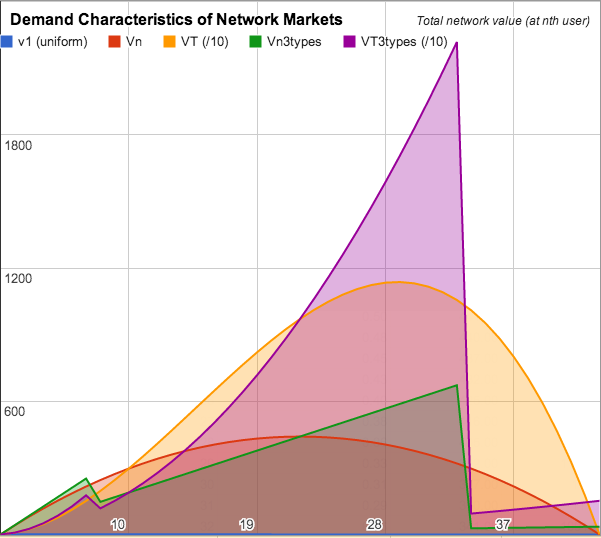 |
| Graph of network value overlaying uniformly distributed demand and 'three types of customer' model |
Labels:
Second Week
Exercise: Metcalfe's Law
Goal To model/graph demand characteristics for network markets in order to understand the assumptions and predictions of economics for network industries. In this case Metcalfe's law.
At least one laptop or tablet running a spreadsheet application for each group.
Individuals or groups of 2 or 3 students working on a single computer.
You will need basic knowledge of: spreadsheet calculations, sum, addition, multiplication, bracket rules, cell ranges, relative cell references, absolute cell references etc.
Up to one hour to complete depending on class size, i.e.
20-30" to create models.
10-20" to present and interpret.
Instructions
Open and save a spreadsheet: enter formulae, values and calculations to create a graph representing a network market valued according to Metcalfe's law.
a) Enter the following data in columns and generate line or scatter graphs:
If there are n people in a network, and the value of the network to each of them is proportional to the number of other users, then the total value of the network (to all users) is proportional to n*(n-1)
(Shapiro & Varian, 1999:p184)Materials
At least one laptop or tablet running a spreadsheet application for each group.
Individuals or groups of 2 or 3 students working on a single computer.
You will need basic knowledge of: spreadsheet calculations, sum, addition, multiplication, bracket rules, cell ranges, relative cell references, absolute cell references etc.
Up to one hour to complete depending on class size, i.e.
20-30" to create models.
10-20" to present and interpret.
Instructions
Open and save a spreadsheet: enter formulae, values and calculations to create a graph representing a network market valued according to Metcalfe's law.
a) Enter the following data in columns and generate line or scatter graphs:
- A column containing an index n representing the number of users e.g. from 1 to 50.
- A column containing the valuation if there is no network value to individuals, i.e. if everyone values product equally i.e. v = 1
- A column containing a valuation for the whole market but no network effect i.e. Vt = n*v
- Next add a column containing a value for the utility/value to nth user of connections to n-1 other users i.e. Vn = v*(n-1)
- Finally, add a column containing a valuation for the whole network market (at n) to all n users i.e. Vtn = n*(v*(n-1))
Your graph should look something like this:
 |
| Metcalfe's Law for a network up to n=5 |
Or this for higher n...
 |
| Metcalfe's Law for a network up to n=56 |
Questions:
What do the models represent?
What does the 'index' represent?
How realistic is Metcalfe's law?
Is it possible for the supplier to monetise the value or utility obtained by users?
How should a supplier price the product or service?
Are physical goods industries applicable to Metcalfe's Law?
Is software inherently a network product or service?
What is the key question for a supplier?
What does the 'index' represent?
How realistic is Metcalfe's law?
Is it possible for the supplier to monetise the value or utility obtained by users?
How should a supplier price the product or service?
Are physical goods industries applicable to Metcalfe's Law?
Is software inherently a network product or service?
What is the key question for a supplier?
Labels:
Second Week
Wednesday, 23 July 2014
Exercise: Information and Market Failures
Goal To create a model/graph depicting necessary conditions for a market to exist when quality is uncertain; in order to understand assumptions and different interpretations for all market models.
Materials
At least one laptop or tablet running a spreadsheet application for each group.
Individuals or groups of 2 or 3 students working on a single computer.
You will need basic knowledge of: spreadsheet calculations, sum, addition, multiplication, bracket rules, cell ranges, relative cell references, absolute cell references etc.
Up to one hour to complete depending on class size, i.e.
20-30" to create models.
10-20" to present and interpret.
Instructions
Open and save a spreadsheet: enter formulae, values and calculations to create a graph of the classic price/demand model.
a) Enter the following data in columns and generate line or scatter graphs:
Questions:
Materials
At least one laptop or tablet running a spreadsheet application for each group.
Individuals or groups of 2 or 3 students working on a single computer.
You will need basic knowledge of: spreadsheet calculations, sum, addition, multiplication, bracket rules, cell ranges, relative cell references, absolute cell references etc.
Up to one hour to complete depending on class size, i.e.
20-30" to create models.
10-20" to present and interpret.
Instructions
Open and save a spreadsheet: enter formulae, values and calculations to create a graph of the classic price/demand model.
a) Enter the following data in columns and generate line or scatter graphs:
- An index, e.g. from 1 to 50.
- A variable q representing the quality of used cars, randomly distributed over the interval [0, 1]. You might use the rand() function to generate this value.
- Assuming buyers are prepared to pay up to 1.5 times the suppliers reserve price... Add a column 1.5*0.5 = 0.75. Valuation if everyone values equally assuming average quality (1/2) then buyers are prepared to pay a hypothetical average price 1.5*0.5 = 0.75
Your graph should look something like this:
 |
| fig 1. The problem of uncertainty and the market mechanism |
b) Add a column for valuation if buyers had perfect quality information and were prepared to pay p = 1.5*q.
Your new graph should look something like this:
 |
| fig 2. If customers had perfect information... |
And if you sort the market index on actual quality the graph should look something like this:
 |
| fig 3. If a potentially perfect buyer/supplier matching mechanism existed... |
Questions:
What do you think the models represent?
What does the 'index' represent?
What changes if you use an index from 1 to 100, 1 to 1,000,000?
Why did use the random number function to generate the quality value?
What is happening if you sort the market index based on actual quality? (other than generate a more appealing graph) Perhaps you are adding something?
What does the 'index' represent?
What changes if you use an index from 1 to 100, 1 to 1,000,000?
Why did use the random number function to generate the quality value?
What is happening if you sort the market index based on actual quality? (other than generate a more appealing graph) Perhaps you are adding something?
Labels:
Second Week
Hermeneutics: Discussing ideas as a style of learning
These sessions emphasise discussion as an ideal style of learning. They provide opportunities for you to discuss the underlying ideas and consequences for the theories set out in the papers. Our intent is not to expect you to untangle the minutiae of complex economic models but to encourage you to appreciate the implications and thrust of the ideas and evidence that underpins them and to consider the consequences for policy and behaviour. We therefore expect you to read the book* from cover to cover, and to read (quickly) the research papers and other selected chapters to build up ideas of their intent and implications (see the syllabus).
(*Shapiro, C. & Varian, H. R. (1998) Information rules : a strategic guide to the network economy, Boston, Mass., Harvard Business School Press.)
Some of the sessions will also be driven with slides in the traditional lecture format. All of the readings, book chapters and books have been very carefully selected. They are paradigm changing exemplars, key contributions to transforming understanding and knowledge of the economic environments that imbricate and constitute aspects of digital goods and markets. Our experience is that the Masters students at UCD really engage with the readings and really involve themselves in good discussions. We expect that you will continue and deepen this tradition.
(*Shapiro, C. & Varian, H. R. (1998) Information rules : a strategic guide to the network economy, Boston, Mass., Harvard Business School Press.)
Some of the sessions will also be driven with slides in the traditional lecture format. All of the readings, book chapters and books have been very carefully selected. They are paradigm changing exemplars, key contributions to transforming understanding and knowledge of the economic environments that imbricate and constitute aspects of digital goods and markets. Our experience is that the Masters students at UCD really engage with the readings and really involve themselves in good discussions. We expect that you will continue and deepen this tradition.
Labels:
Second Week
Exercise: Demand Curves
Goal
To create a graph of the classic price/demand model in order to understand assumptions and different interpretations of the model.
Materials
At least one laptop or tablet running a spreadsheet application for each group.
Individuals or groups of 2 or 3 students working on a single computer.
You will need basic knowledge of: spreadsheet calculations, sum, addition, multiplication, bracket rules, cell ranges, relative cell references, absolute cell references etc.
Up to one hour to complete depending on class size, i.e.
20-30" to create models.
10-20" to present and interpret.
Instructions
Open and save a spreadsheet: enter formulae, values and calculations to create a graph of the classic price/demand model.
a) Enter the following data in columns and generate line or scatter graphs:
b) Add a unit demand function representing the classic 'three types of customer' model i.e. with value/demand/utility [1.0, 0.5, 0.02]; of the following ratios: Spend Thrifts 10% (v=1.0), Average Spenders 60% (v=0.5), Tight Wads 30% (v=.02).
c) Add a demand function representing where 'Everyone Values Equally ', i.e. v=1 for all.
Your models should look something like this:
Questions:
What do you think the models represent?
What does the 'index' represent?
What changes if you use an index from 1 to 100, 1 to 1,000,000?
What if you plotted values using a scatter chart rather than a line chart?
Why use the range 0-1 for utility/demand/value?
What does the idea of demand represent?
What does idea of value represent?
What does the idea of utility represent?
Is it reasonable to use the concepts interchangeably?
What does this model assume about the possible market of consumers or buyers?
Does this model represent actual consumers or buyers? What assumptions about buyers are being made?
Does this model describe both products and services?
Does this model describe both physical and digital goods?
What is a market?
How big is the market? What assumptions are you making?
What is the relationship between market price and demand?
How would you represent the relationship between price and demand? Is it realistic?
What price would the supplier like to set? What assumptions are you making?
What price would you recommend to the supplier to set? Why?
What changes if other suppliers enter the market?
Comments
May use MS Excel, Google docs spreadsheet, OpenOffice, Numbers.
Materials
At least one laptop or tablet running a spreadsheet application for each group.
Individuals or groups of 2 or 3 students working on a single computer.
You will need basic knowledge of: spreadsheet calculations, sum, addition, multiplication, bracket rules, cell ranges, relative cell references, absolute cell references etc.
Up to one hour to complete depending on class size, i.e.
20-30" to create models.
10-20" to present and interpret.
Instructions
Open and save a spreadsheet: enter formulae, values and calculations to create a graph of the classic price/demand model.
a) Enter the following data in columns and generate line or scatter graphs:
- An index, e.g. from 1 to 50.
- A demand function for each person, uniformly distributed over the interval [0, 1] i.e.: 1, 0.98, 0.96, ..., 0.02, 0.0.
b) Add a unit demand function representing the classic 'three types of customer' model i.e. with value/demand/utility [1.0, 0.5, 0.02]; of the following ratios: Spend Thrifts 10% (v=1.0), Average Spenders 60% (v=0.5), Tight Wads 30% (v=.02).
c) Add a demand function representing where 'Everyone Values Equally ', i.e. v=1 for all.
Your models should look something like this:
 |
| 3 different value/demand/utility models |
What do you think the models represent?
What does the 'index' represent?
What changes if you use an index from 1 to 100, 1 to 1,000,000?
What if you plotted values using a scatter chart rather than a line chart?
Why use the range 0-1 for utility/demand/value?
What does the idea of demand represent?
What does idea of value represent?
What does the idea of utility represent?
Is it reasonable to use the concepts interchangeably?
What does this model assume about the possible market of consumers or buyers?
Does this model represent actual consumers or buyers? What assumptions about buyers are being made?
Does this model describe both products and services?
Does this model describe both physical and digital goods?
What is a market?
How big is the market? What assumptions are you making?
What is the relationship between market price and demand?
How would you represent the relationship between price and demand? Is it realistic?
What price would the supplier like to set? What assumptions are you making?
What price would you recommend to the supplier to set? Why?
What changes if other suppliers enter the market?
Comments
May use MS Excel, Google docs spreadsheet, OpenOffice, Numbers.
Labels:
Second Week
Reading exercises: Location for class interpretations
Labels:
Second Week
Tuesday, 22 July 2014
6. Network Externalities
We now deal with the Network Effect. Economists have studied similar effects for a generation and call them Externalities. These are the situations when production or consumption affect people who are not directly involved in these transactions. The classical examples were about pollution (a negative externality) and education (positive, I hope). Since the mid 1970s there is an interest in externalities in communication and technology networks. The first paper about this effect was published in 1974 by Jeffery Rohlfs from Bell Labs.
This paper from 1985 is the famous model of network externalities and competition by Katz and Shapiro from the University of California in Berkley. The paper presents the basis for our current business thinking about competition and compatibility in Information Technology.
Now it is clear that handling correctly the network effect is critical to success in technology markets. Apple is a good example. During the 1980s, Apple hesitated a long time between controlling and opening its Mac technology. Should it allow others to build and sell the hardware? Should it allow others to develop and sell software for the Macintosh? They had a few false starts with openness but finally chose a control strategy rather than letting go of control and letting the market create a much larger network. At the end of this period Apple's market share was 3% while the IBM compatible market held by Microsoft and Intel had the rest. Apple and Steve Jobs got an opportunity to rethink their network effect strategy with a hand held communication and computing devise they introduced six years ago. What strategy do you think they used? During the early 2000s it was clear that some openness is critical and we got the App Store and hundreds of thousands of applications for this technology.
These ideas are extremely practical and important for the management of technology but the paper is also important because it is analytical and applicable to your own organisations, for example understanding how to go about setting price to maximise profit. Thanks to Katz and Shapiro we can play with a mathematical model and experiment with pricing and network size. In this class we will limit ourselves to the problems of pricing and market expectation formation of a single supplier by building our own simple model of monopoly in a communication service.
If you wish to explore this paper and competition in markets with network externalities more deeply you should familiarise yourself with Cournot (en.wikipedia.org/wiki/Cournot_competition).
This paper from 1985 is the famous model of network externalities and competition by Katz and Shapiro from the University of California in Berkley. The paper presents the basis for our current business thinking about competition and compatibility in Information Technology.
Now it is clear that handling correctly the network effect is critical to success in technology markets. Apple is a good example. During the 1980s, Apple hesitated a long time between controlling and opening its Mac technology. Should it allow others to build and sell the hardware? Should it allow others to develop and sell software for the Macintosh? They had a few false starts with openness but finally chose a control strategy rather than letting go of control and letting the market create a much larger network. At the end of this period Apple's market share was 3% while the IBM compatible market held by Microsoft and Intel had the rest. Apple and Steve Jobs got an opportunity to rethink their network effect strategy with a hand held communication and computing devise they introduced six years ago. What strategy do you think they used? During the early 2000s it was clear that some openness is critical and we got the App Store and hundreds of thousands of applications for this technology.
These ideas are extremely practical and important for the management of technology but the paper is also important because it is analytical and applicable to your own organisations, for example understanding how to go about setting price to maximise profit. Thanks to Katz and Shapiro we can play with a mathematical model and experiment with pricing and network size. In this class we will limit ourselves to the problems of pricing and market expectation formation of a single supplier by building our own simple model of monopoly in a communication service.
If you wish to explore this paper and competition in markets with network externalities more deeply you should familiarise yourself with Cournot (en.wikipedia.org/wiki/Cournot_competition).
Monday, 21 July 2014
5. Efficient Capital Markets (TCE)
We now start getting to grips with Transaction Cost Economics (TCE). If you doubt how practical the ideas of Information Economics are, you should not doubt the practicality of TCE. Malone, Yates and Benjamin (1989) were implicitly using TCE to explain how the world of business would change because of 'electronic markets' and what businesses have to do about it.
Williamson is viewed by many, particularly scholars of Strategy and Marketing, to be the father of Transaction Cost Economics (TCE), however Williamson's work was based upon the discoveries of Ronald Coase and others.
Being first with the idea or its elaboration pays off, even if it seems obscure is difficult to read, slow to gel. This early article by Oliver E. Williamson expanded upon Coase's work, then 20 years old, to further understand how transaction cost economics may account for different organisational forms. For this Williamson shared the Sveriges Riksbank Price in Economic Sciences in Memory of Alfred Nobel 2009. Elinor Ostrom for her 'analysis of economic governance, especially the commons', subject matter for another course. Williamson 'for his analysis of economic governance, especially the boundaries of the firm'.
The paper was worked into the first chapters of Williamson's influential 'Markets and Hierachies: Analysis and Antitrust Implications' (1975).
Williamson is viewed by many, particularly scholars of Strategy and Marketing, to be the father of Transaction Cost Economics (TCE), however Williamson's work was based upon the discoveries of Ronald Coase and others.
Being first with the idea or its elaboration pays off, even if it seems obscure is difficult to read, slow to gel. This early article by Oliver E. Williamson expanded upon Coase's work, then 20 years old, to further understand how transaction cost economics may account for different organisational forms. For this Williamson shared the Sveriges Riksbank Price in Economic Sciences in Memory of Alfred Nobel 2009. Elinor Ostrom for her 'analysis of economic governance, especially the commons', subject matter for another course. Williamson 'for his analysis of economic governance, especially the boundaries of the firm'.
The paper was worked into the first chapters of Williamson's influential 'Markets and Hierachies: Analysis and Antitrust Implications' (1975).
4. The Nature of the Firm (the grandfather of TCE)
Information technology has had, and continues to have, a disruptive and transformative impact on the organisation of firms, markets, and whole economies. But without a theory of what firms are and why they arise we cannot really understand why firms exist, after all, if market mechanisms are the bedrock of capitalist production why do firms exist at all? Is it technological determinism, the deus ex machina, or can we identify constructs and structures that matter?
Ronald Coase's 1937 paper addressed existential questions on nature of the firm. Coase -- died aged 102 in 2013 -- was then 27 years old and had the brilliance and Chutzpa to ask and answer a fundamental question -- why companies exist? In what ways are firms better ways of organising production and exchange than markets? The answer he concludes lies in what we now term Transaction Costs -- the costs of going to the market. He wrote about 'the cost of organising an extra transaction' (Coase, 1937:p396) versus 'the costs involved in leaving the transaction to be "organised" by the price mechanism.' (Coase, 1937:p404). He called them Marketing Costs, but this was 1937 and he didn't mean 'marketing' as we do. Namely, the costs of searching for information about products, prices, vendors. Yes, information again. Transaction costs include also the costs of bargaining, contracting, etc.
This paper has had immense impact in the field of Economics. However Coase waited more than 60 years for the ultimate recognition. You should watch his 2003 Coase Lecture. You would not expect a lecture by a very old professor of Economics to be funny, but it is.
Some questions to think about:
Q: Would Coase have argued that a postal service should or should not be 'bundled' with for-profit goods and services such as banking or insurance, and competing where the markets and industry can easily provide them instead?
A: Should also unbundle the infrastructure paid for by citizens before selling off bits that the state gives unfair advantage to (semi-state monopoly co's). You can be sure that industry doesn't really want to operate a universal postal service unless it gets handsome subsidies.
Ronald Coase's 1937 paper addressed existential questions on nature of the firm. Coase -- died aged 102 in 2013 -- was then 27 years old and had the brilliance and Chutzpa to ask and answer a fundamental question -- why companies exist? In what ways are firms better ways of organising production and exchange than markets? The answer he concludes lies in what we now term Transaction Costs -- the costs of going to the market. He wrote about 'the cost of organising an extra transaction' (Coase, 1937:p396) versus 'the costs involved in leaving the transaction to be "organised" by the price mechanism.' (Coase, 1937:p404). He called them Marketing Costs, but this was 1937 and he didn't mean 'marketing' as we do. Namely, the costs of searching for information about products, prices, vendors. Yes, information again. Transaction costs include also the costs of bargaining, contracting, etc.
This paper has had immense impact in the field of Economics. However Coase waited more than 60 years for the ultimate recognition. You should watch his 2003 Coase Lecture. You would not expect a lecture by a very old professor of Economics to be funny, but it is.
Some questions to think about:
Q: Would Coase have argued that a postal service should or should not be 'bundled' with for-profit goods and services such as banking or insurance, and competing where the markets and industry can easily provide them instead?
A: Should also unbundle the infrastructure paid for by citizens before selling off bits that the state gives unfair advantage to (semi-state monopoly co's). You can be sure that industry doesn't really want to operate a universal postal service unless it gets handsome subsidies.
Sunday, 20 July 2014
3. The Market for Lemons (information asymmetry)
This seminal paper by George Akerlof is elegant and easy to read. The style of the paper is very different from Fama's paper on the EMH.
Akerlof starts with a mundane question: why are used cars are so much cheaper than new cars? As this is a course about the Economics of Information (Technology), you can guess the answer -- something about information? There are good cars (cherries) and bad cars (lemons), and some of the participants in the market have more information than others .. please read the paper for the full answer.
The history of this paper is very interesting. It was rejected for its 'triviality' by both the American Economic Review and the review of Economic Studies. It was rejected for being incorrect by the reviewers from the Journal of Political Economy.
It turns out that this is one the most cited papers in Economics, it is one of the first works to study markets with asymmetric information and it is the one paper mentioned by the Noble Prize committee when they announced Akerlof's prize ... what a trivial paper!
A nice question for the exam may be about the Tax problems of Henry VIII. He replaced almost half of the silver in coins with base metals, to increase the government's income without raising taxes. Merchants knew that and saved the old pure silver shillings while circulating the bad ones. Namely bad money drove out good money and this has become to be known as Gresham's law. Is this story the same as Akerlof's story about cars and lemons? The answer is in the paper.
Akerlof starts with a mundane question: why are used cars are so much cheaper than new cars? As this is a course about the Economics of Information (Technology), you can guess the answer -- something about information? There are good cars (cherries) and bad cars (lemons), and some of the participants in the market have more information than others .. please read the paper for the full answer.
The history of this paper is very interesting. It was rejected for its 'triviality' by both the American Economic Review and the review of Economic Studies. It was rejected for being incorrect by the reviewers from the Journal of Political Economy.
It turns out that this is one the most cited papers in Economics, it is one of the first works to study markets with asymmetric information and it is the one paper mentioned by the Noble Prize committee when they announced Akerlof's prize ... what a trivial paper!
A nice question for the exam may be about the Tax problems of Henry VIII. He replaced almost half of the silver in coins with base metals, to increase the government's income without raising taxes. Merchants knew that and saved the old pure silver shillings while circulating the bad ones. Namely bad money drove out good money and this has become to be known as Gresham's law. Is this story the same as Akerlof's story about cars and lemons? The answer is in the paper.
Saturday, 19 July 2014
2. Efficient Market Hypothesis (EMH)
The Efficient Market Hypothesis is the second item in our very small selection of papers about Information in Economics. The idea is simple -- prices on traded assets reflect the information available in the markets. So, markets are information-ally efficient.
It probably should have been the first item in this course as this idea is possibly the most influential concept in contemporary Economics. Many would say the most damaging concept.
The original paper by Eugene Fama from 1965 is so long that we selected a later paper by Fama, his review from 1970. It is still a long and complex paper, we have highlighted selected several paragraphs for reading.
The style of the paper is very different from our next reading, Akerlof's elegant Market for Lemons.
Fama deals with empirical research of complex phenomenon with a lot of data, so elegance of writing is not possible. But the idea that markets are efficient is so attempting and influential that the effort in reading parts of the paper is worthwhile.
We have also considered the recent arguments against and for this hypothesis as reflected by The Economist.
It probably should have been the first item in this course as this idea is possibly the most influential concept in contemporary Economics. Many would say the most damaging concept.
The original paper by Eugene Fama from 1965 is so long that we selected a later paper by Fama, his review from 1970. It is still a long and complex paper, we have highlighted selected several paragraphs for reading.
The style of the paper is very different from our next reading, Akerlof's elegant Market for Lemons.
Fama deals with empirical research of complex phenomenon with a lot of data, so elegance of writing is not possible. But the idea that markets are efficient is so attempting and influential that the effort in reading parts of the paper is worthwhile.
We have also considered the recent arguments against and for this hypothesis as reflected by The Economist.
Friday, 18 July 2014
1. The Logic of Electronic Markets
This is our first paper and it sets up problems and assumptions that we address in the remainder of the course. It is a short readable article by three researchers from MIT boosting the idea that electronic markets will supplant firms' internal systems and displace buyer-seller relationships to electronic markets.
Claims stated include: reduced transaction and contracting costs, commoditisation, operational cost savings, lower prices, increased competitive advantage for 'winners', reduced vertical integration of firms, disintermediation of physical by electronic suppliers, benefits of standardisation (go-it-alone or industry agreements),
Implied in the argumentation is the application of Transaction Cost Economics (TCE). They apply the ideas of TCE to the potentialities of 'electronic buyer-seller connections'.
In other publications they analysed the transaction costs and the possibility of 'hold-up' (or lock-in) to predict in detail the emergence of 'electronic markets' ten years in advance. The logic of electronic markets predicts that smaller companies will arise. In three US sectors the authors checked, the prediction has not been supported. We've put also on the portal a recent article from the Economist that seems to support TCE ideas.
However in order to fully understand the reasoning of Malone, Yates and Benjamin, it is essential to know a little bit about foundational economics concepts, about markets, models of utility and buyer-seller relationships. The structure of the remaining readings addresses this as follows:
Claims stated include: reduced transaction and contracting costs, commoditisation, operational cost savings, lower prices, increased competitive advantage for 'winners', reduced vertical integration of firms, disintermediation of physical by electronic suppliers, benefits of standardisation (go-it-alone or industry agreements),
Implied in the argumentation is the application of Transaction Cost Economics (TCE). They apply the ideas of TCE to the potentialities of 'electronic buyer-seller connections'.
In other publications they analysed the transaction costs and the possibility of 'hold-up' (or lock-in) to predict in detail the emergence of 'electronic markets' ten years in advance. The logic of electronic markets predicts that smaller companies will arise. In three US sectors the authors checked, the prediction has not been supported. We've put also on the portal a recent article from the Economist that seems to support TCE ideas.
However in order to fully understand the reasoning of Malone, Yates and Benjamin, it is essential to know a little bit about foundational economics concepts, about markets, models of utility and buyer-seller relationships. The structure of the remaining readings addresses this as follows:
- The assumptions of how markets and the market-price-mechanism works (Eugene F. Fama).
- How markets may fail and how buyers and sellers deal with uncertainty (George A. Akerlof).
- To deeply understand the relationship between the organisation of markets and firms through the discovery and nature of transaction costs and property rights (Ronald H. Coase).
- ...culminating in the development of transaction cost economics to account for different organisational forms (Oliver E. Williamson).
- Finally we look at some characteristics of network industries and assumptions around supply, demand, utility, value and price (Michael L. Katz and Carl Shapiro).
Information Economics, Transaction Cost Economics, Externalities
Revised readings and structure
Economic theory about the role of information in markets has grown dramatically during the last decades. We will review some seminal economics articles presenting first principles treatments of economics theories of organisation, firms and markets.- MaloneEtAl, The Logic of Electronic Markets, 1989.
- Fama, Efficient Capital Markets, 1970.
- Akerlof, The Market for Lemons, 1970.
- Coase, The Nature of the Firm, 1939.
- Williamson, Markets and Hierarchies, 1973.
- KatzShapiro, Network Externalities Competition Compatibility, 1985.
Our first paper sets up problems and assumptions that we address in the remainder of the course. It is a short readable article by three researchers from MIT boosting the idea that electronic markets will supplant firms' internal systems and displace buyer-seller relationships to electronic markets.
Implied in the argumentation is the idea of markets, firms, networks and Transaction Cost Economics (TCE) and their potentialities for the economics of Information Technology and Digital Markets. It is essential therefore to know a little bit about foundational economics concepts, about markets, models of utility and buyer-seller relationships. The structure of the remaining readings addresses this as follows:
• The assumptions of how markets and the market-price-mechanism works (Eugene F. Fama).
• How markets may fail and how buyers and sellers deal with uncertainty (George A. Akerlof).
• To deeply understand the relationship between the organisation of markets and firms through the discovery and nature of transaction costs and property rights (Ronald H. Coase).
• ...culminating in the development of transaction cost economics to account for different organisational forms (Oliver E. Williamson).
• Finally we look at some characteristics of network industries and assumptions around supply, demand, utility, value and price (Michael L. Katz and Carl Shapiro).
Shapiro and Varian's book "Information Rules: A Strategic Guide to the Network Economy" (1999), is background reading. Chapters may be discussed if time allows.
Labels:
Second Week
Subscribe to:
Comments (Atom)